The Rule of 3 + 9
The rules of 4 and 2 are well documented as quick and easy methods for converting the number of outs (on the flop or turn) into an approximate percentage probability of hitting your outs. I assume you have heard of these rules. If not, I have previously written an article explaining the rule of 4 and 2.
Briefly, the Rule of 4 is used by poker players on the flop to determine the probability of hitting a draw by the river. You multiply the number of outs by 4 and this is taken as an approximate percentage of your chance of hitting your draw on the turn or river.
In a previous article, I explained simple adjustments for getting the Rule of 2 more accurate. The standard Rule of 4 is even more inaccurate than the Rule of 2.
In this article, I am going to discuss how to improve the accuracy of the Rule of 4 using a simple adjustment that I have named the “Artimus Adjustment”.
Exact Percentages
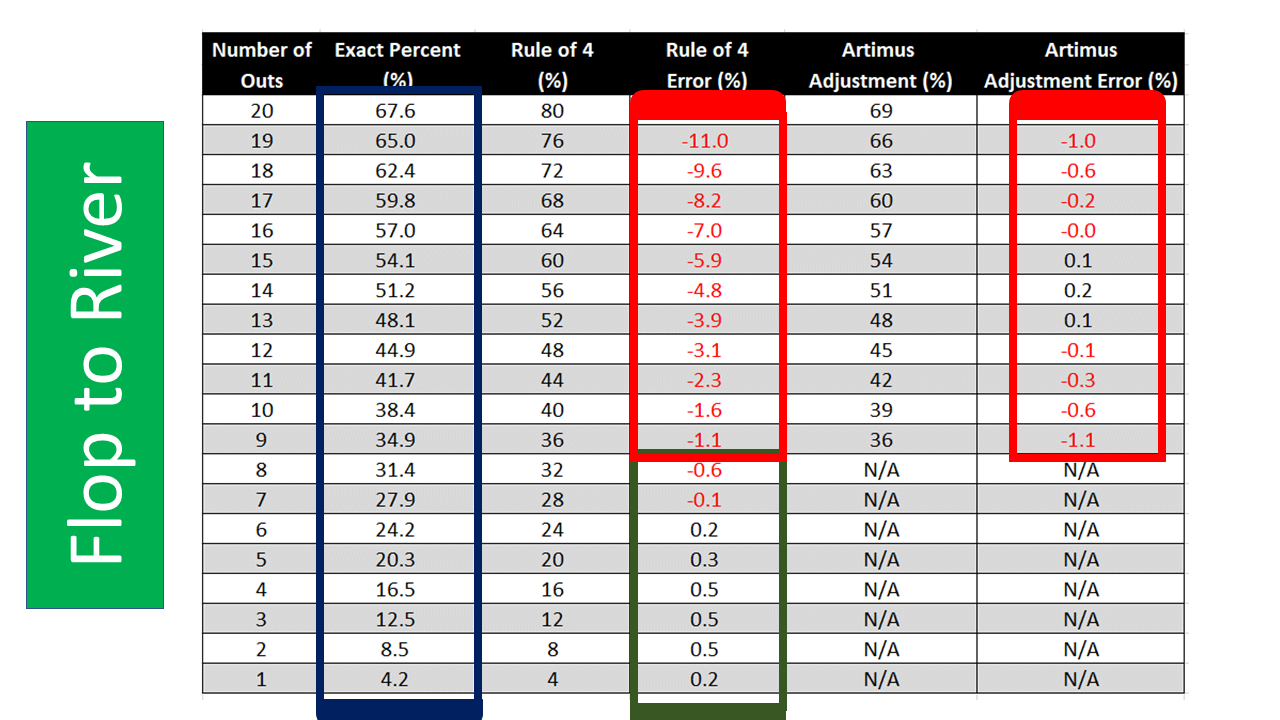
In the Table below, you can see the exact percentage of hitting your outs in column 2. The way this is calculated is by calculating the chances of not hitting your outs on the flop and turn. Then. Subtracting this number from 1.
For example (using Tables 1 and 2 from my Rule of 2.1 and 2.2 article), the chance of hitting 15 outs is 0.319 on the turn and 0.326 on the river.
The chance of not hitting your outs on either street is (1 – 0.319) x (1 – 0.326) = 0.459.
Then, 1 – 0.459 = 0.541, which is 54.1%.
Problems with the Rule of 4
Column 3 of Table 1 shows the difference between the exact percentage and the percentage obtained by using the Rule of 4.
As you can see, the method is accurate up to 8 outs. Beyond that, then method starts to fall apart. Ideally, we want to be within 1% of the exact percentage.
We shouldn’t be too worried about the very high number of outs. You will only know you have 20 outs on the flop if you are some kind of master hand reader or you have had a peek at your opponent’s hand. However, the numbers between 9 and 15 outs are important.
At 9 outs, the Rule of 4 is 1.1% inaccurate. At 15 outs, it is 5.9% inaccurate. This is unacceptable. I’ve read articles written by poker gurus, who say it doesn’t matter because, with 15 outs, you are a favourite with over a 50% of hitting your draw. Therefore, you can shove anyway.
No, you can’t. Calculating the probability of hitting your outs is not the same as calculating your probability of winning the hand. We are playing against ranges.
Ranges include sets. Against sets, you have the problem of the board pairing.
Ranges also include nut flush draws. When you have an open-ended straight draw and a flush draw, you never have the nut flush draw. Therefore, you might just have a straight draw that can be outdrawn by a better flush.
When you have a non-nut flush draw, you also have the problem of the flush suit hitting on both the turn and river. If your opponent has the ace (or any higher card than you have of the flush suit), you will lose.
Such scenarios are not accounted for in the Rule of 4.
You will often need further calculations to determine your probability of winning a hand. That’s a big topic that will not be dealt with here.
The main point is that you need to calculate a probability that is close to the real number.
We will now look at how to get closer to the exact percentage.
The Artimus Adjustment
I have devised a simple method of getting from the Rule of 4 to within 1% (in most cases) to the exact percentage.
The magic number is 9. The Rule of 4 works up to 8 outs. Therefore, we will only apply the Artimus Adjustment to 9 or more outs. That is not the reason that the magic number is 9.
So, this is how it works:
Step 1: Calculate your probability by the Rule of 4
Step 2: Add 9 to this score
Step 3: Subtract the number of outs from this score
Steps 2 and 3 are the Artimus Adjustment.
Example: You have 15 outs
Step 1: Using the Rule of 4: 15 x 4 = 60
Step 2: Add 9: 60 + 9 = 69
Step 3: Subtract the number of outs: 69 – 15 = 54
The fifth column of Table 1 shows the percentages calculated using the Artimus Adjustment. The sixth column shows how far this score is from the exact score. As you can see, all scores are with 1% of the exact score, except for 9, 19 and 20 outs.

Conclusion
You will never have 19 or 20 clear outs on the flop. Therefore, if you just remember to subtract 1% for 9 outs and use the Artimus Adjustment for the higher number of outs, your calculations will be within 1% of the exact percentage,